Compact Covers of Orientable Surfaces

The following question was asked to my friend during an interview for the Oxford PhD program:

(Characterize the Compact Covers of Compact Orientable Surfaces) Given a compact orientable surface $\mathcal S$, what do its (compact) covers look like? More specifically, if $\mathcal S$ has genus $k$, what are the conditions on $n$ if another compact orientable surface $\mathcal S'$ of genus $l$ covers $\mathcal S$, i.e what are the possible pairs $(k,l)$?

The answer came pretty fast because I had been thinking about the same problem for different reasons. For some reason it took me a while to feel at ease with the lifting criterion:

(Lifting Criterion) Suppose we are handed a covering space $p: (\tilde{X}, \tilde{x_0}) \rightarrow (X, x_0)$ and a map $f:(Y,y_0) \rightarrow (X, x_0)$, with $Y$ path-connected and locally path-connected. Then there exists a lift $\tilde{f} :(Y, y_0) \rightarrow (\tilde{X}, \tilde{x_0})$ of $f$ if and only if $f_*(\pi_1(Y,y_0))\subset p_*(\pi_1(\tilde{X},\tilde{x_0}))$.

I think the biggest problem for me was the fact that I intuitively thought the induced map of a covering map $p_* : \pi_1(\tilde{X},\tilde{x_0}) \rightarrow (X,x_0)$ ought to be surjective and not injective.

The proof of injectivity is very easy: a loop $[\tilde{f_0}]$ upstairs in the cover is in the kernel of $p_*$ if it is represented by a loop $\tilde{f_0}:I\rightarrow \tilde{X}$ with a homotopy $f_t:I\rightarrow X$ of $f_0=p\tilde{f_0}$ to the trivial loop. There is a unique lift of that homotopy $\tilde{f_t}$ which goes from $\tilde{f_0}$ to a constant loop (lifts of constant paths are constant), done.

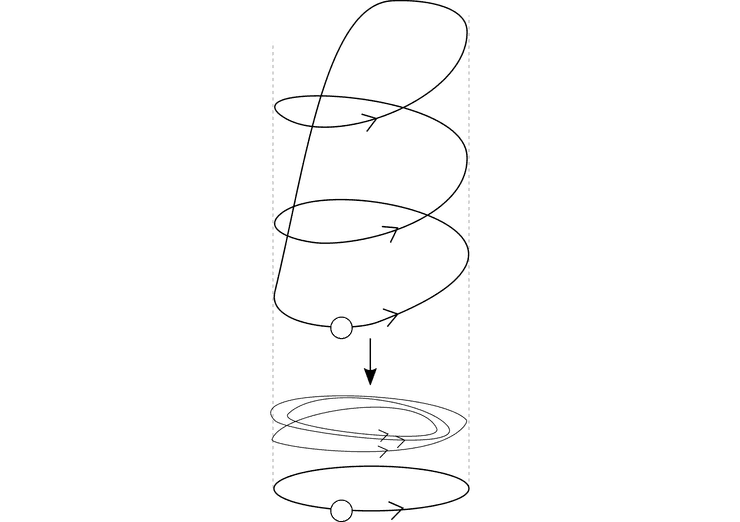
But I was still weirded out precisely because of the examples we’re about to cook up to answer the original question, e.g. the genus 3 surface covering the genus 2 surface. It seems like there are a lot more loops in the genus 3 surface than in the genus 2 surface (I mean, there are more), shouldn’t the induced map be surjective? The answer is no, because of the following very important point: we’re looking at based loops. Before going over the examples, notice that the situation is clear for $k$-sheeted covers of the circle, the image subgroup of the induced map on the fundamental groups is just the subgroup $k\mathbb Z$, as seen in the following picture for $k=3$.

So injectivity is very natural on that example, but I thought less so for surfaces. Let’s take a look at the following example to see how things work for surfaces.

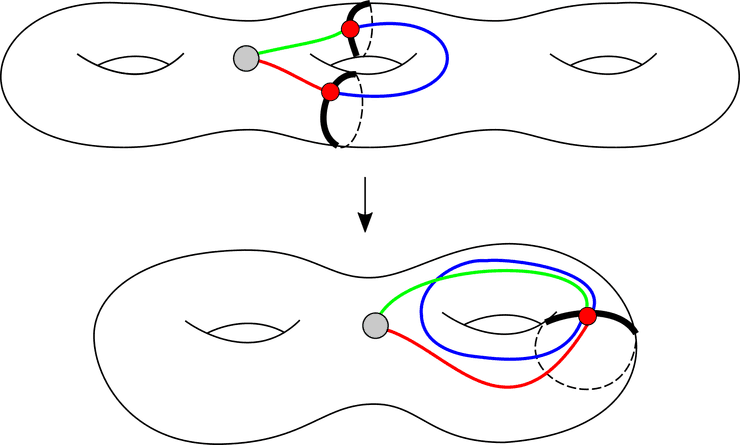
First off, the genus 3 surface covers the genus 2 surface with the two bold black circle identified and the two “branches” being projected to the genus 2 surface. Looking at the loop going once around the middle circle[^Pick one of two directions and stay consistant] of the genus 3 surface (the covering space) we see that by construction this yields a loop going around twice in the genus 2 surface downstairs. That way we see that the image subgroup under $p_*$ here would be $\mathbb Z \times 2\mathbb Z$ for this example.

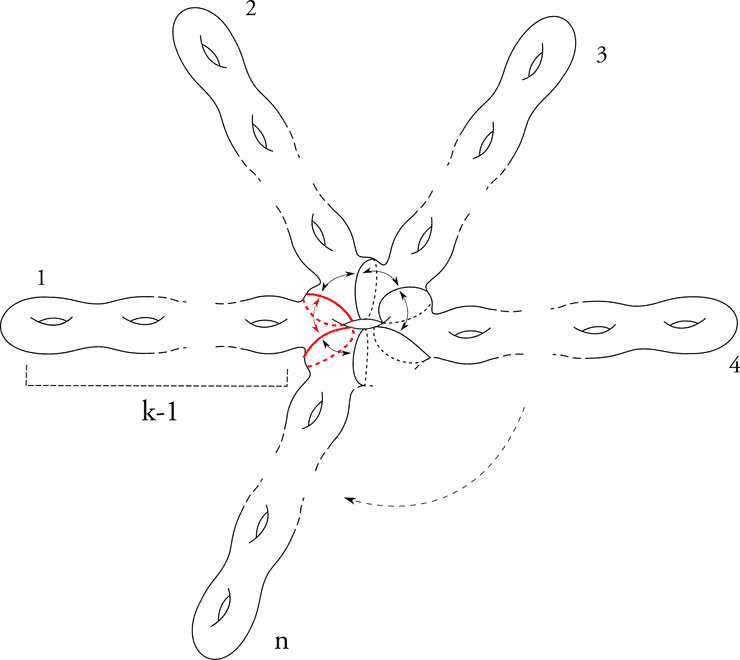
The previous construction can be adapted for $\mathcal S$ of genus $k$: pick any handle and make it the “core” handle of the covering surface. Then add say $n$ branches of genus $(k-1)$ to get the $n$-sheeted cover of $\mathcal S$. Identification around the core handle is done in the same fashion.

This gives us the following result and answers the original question:

(Characterization of the Compact Covers of Compact Orientable Surfaces) Given a compact orientable surface $\mathcal S$ of genus $k$, the compact orientable covers of $\mathcal S$ are exactly the surfaces of genus $l=n(k-1) +1$, $n\geq 2$.

Proof. The existence is given by our previous discussion and the previous figure. Unicity follows for Euler characteristic considerations since in a $n$-sheeted cover, the cardinalities of the set of vertices, edges and faces are all multiplied by $n$.