Cover Time of the Cycle Graph

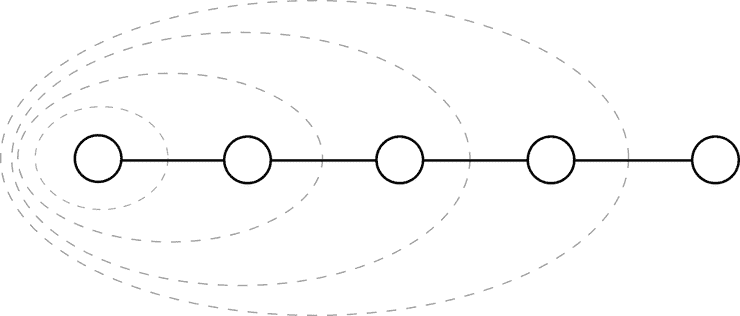
1. Cover Time of the Line Graph

Computing the cover time of the line graph is straightforward using Moon’s lemma.

---

(Moon’s Lemma, 1973) Given a graph for which $(i,j)$ is a cut edge, we have:

where $(S,E)$ is the graph containing $i$ when the edge $(i,j)$ is removed. In particular, if $(S,E)$ is a tree, then:

---

Proof. Traversing the edge $(i,j)$ takes one time step. How many times do we need to come back to $i$ before crossing this bridge? Well, this number of times $N$ is geometrically distributed and we have:

where $d$ is the degree of the node $i$. Now the expected time spent walking in $S$ is just $N \mathbb E T_{ii}$ if by $\mathbb E T_{ii}$ we have in mind a random walk happening on $(S,E)$. If we note $(\pi_1, \ldots, \pi_n)$ the stationnary distribution where $n$ is the number of nodes in $S$, we have (by the property of mean recurrence times) that:

since the degree of the node $i$ is one less in $(S,E)$. Since $N$ is geometric, we also now that $\mathbb E N=d-1$, which yields the proof.

A line graph is of course a tree and we can apply the second equation successively as we move from the left-most vertex to the right-most vertex.

We therefore get a sum of successive odd integers $(2|S|-1)$ as $S$ grows from being the left-most vertex to being the entire line graph:

2. Hitting Time of the Cycle Graph