Given a set of points $X$ together with a metric $d$ , an $\epsilon$ -set $N\subseteq X$ is a set of point such that for every point $x\in X$ , there exists a point $n(x)\in N$ such that $d(x,n(x))\leq\epsilon$ . It is a classical problem of discrete and computational geometry to find $\epsilon$ -nets of small size. In the late 1980s, Haussler and Welzl showed bounds on the size of such sets in the realm of much more abstract and less geometric sets of points, using only the finiteness of their VC-dimension. Their result shows that sets of VC-dimension at most $d$ behave much like Euclidean balls of dimension $d$ .

This write-up with Lucy Davidson contains an intuitive proof of the Primal Shatter Lemma (or Sauer-Shelah-Perlas Lemma) and the easiest proof I know of Haussler’s packing lemma.

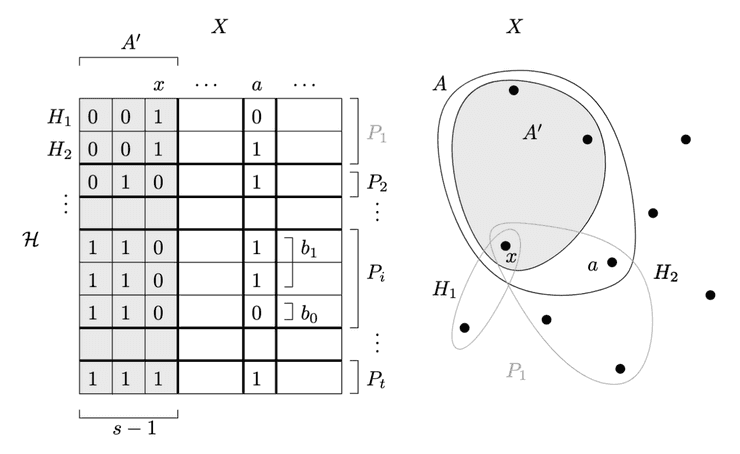
(Primal Shatter Lemma) Let $X$ be a set of $n$ elements and $\mathcal H = \{H_1, H_2, \ldots, H_m\}$ be a set system of VC dimension $d$ on $X$ . For all $A \subseteq X$ , we have
$|\mathcal H_{|A}| \leq \sum_{i=0}^{d} \binom{|A|}{i}$
When $|A| \geq d$ , the previous sum can be upper bounded by $\left(\frac{e|A|}{d}\right)^d = O(|A|^d)$ .

(Haussler’s Packing Lemma) Let $X$ be a set of $n$ elements and $\mathcal H=\{H_1, H_2, \ldots, H_m\}$ be a set system of VC dimension $d$ on $X$ . If $\mathcal H$ is $\epsilon$ -separated then: $|\mathcal H| = O\left(\left(\frac{n}{\epsilon}\right)^d\right)$ .

Packing Set Systems of Finite VC dimension