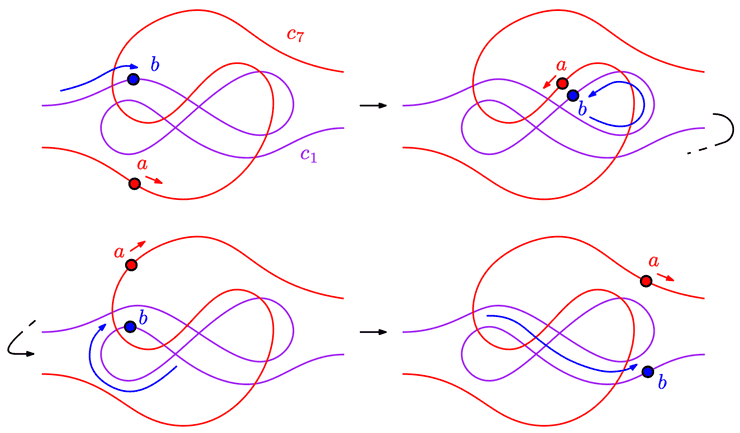
A curve with rotation number one that is not universal for beacon routing
| Authors | Florestan Brunck, Maarten Loffler, Rodrigo I. Silveira |
| Journal | Submitted |
| Publication | September 2025 |
| Link | Read Article |
| Categories | Computational Geometry, Topology, Complexity, Curves, Beacon Routing |
Beacon routing is the study of how to indirectly route objects through various domains. Consider two points —which we think of as the attractor—and —which we think of as the ball—lying on a smooth closed curve in the plane. In curve-restricted beacon routing, moves along the curve as long as its Euclidean straight-line distance to a decreases, until this distance is locally minimal. Assuming moves infinitely faster than a, the goal is to move a along the curve in such a way that a ends up meeting . We say that a curve is universal if there always exists a strategy to catch the ball from every initial configuration of the attractor and the ball. Recent work of Abrahamsen et al. has shown that every simple curve is universal. The authors also conjectured that all curves with rotation number one are universal. In this note, we disprove their conjecture and present a curve with rotation number one that is not universal.