Non-Obtuse Triangulations with Few Steiner Points
| Authors | Mikkel Abrahamsen, Florestan Brunck, Jacobus Conradi, Benedikt Kolbe, André Nusser |
| Journal | SoCG |
| Publication | December 2024 |
| Link | Read Article |
| Categories | Computational Geometry, Algorithm, Non-Obtuse Triangulation |
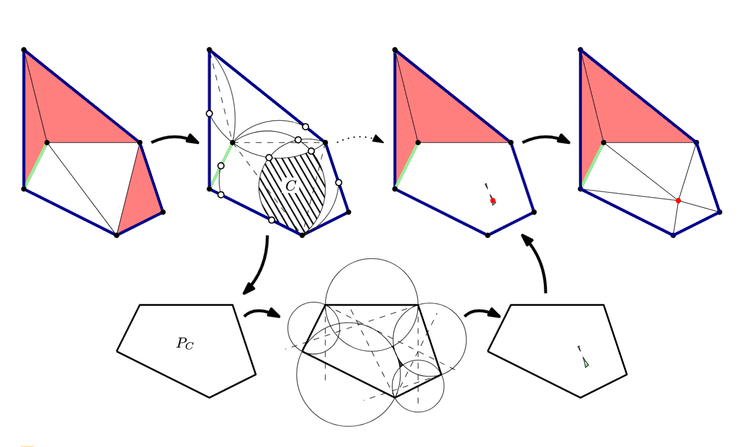
In late 2024, Mikkel Abrahamsen, Jacobus Conradi, Benedikt Kolbe, André Nusser and I teamed up for the 7th edition of the CG:SHOP competition. The challenge this time was to produce high quality triangulations of a set of planar straight line graphs (PSLGs), in which each triangle is non-obtuse. The goal was producing such triangulations with as few Steiner points as possible. We placed first in this competition and were invited to present our algorithm at SoCG 2025.
Our approach involves a local search in the space of all triangulations by computing a small set of candidate Steiner points. The algorithm then picks one of these candidate Steiner points based on a game-tree inspired evaluation function to be introduced into the current triangulation. This step is then repeated until no obtuse triangle is left in the triangulation. We find that on the provided instances we typically use less Steiner points than the number of input vertices in the planar straight line graph. This is a stark contrast to the best known theoretical upper bound due to Christopher Bishop.
The paper is yet to be available but Jacobus made the code available on this github repository.