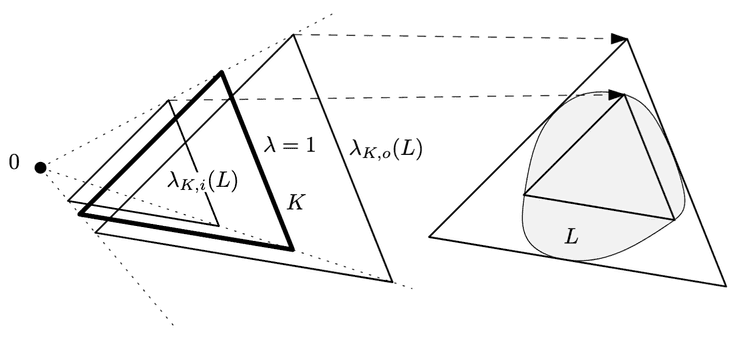Approximate Depth of Convex polytopes
| Authors | Egor Bakaev, Florestan Brunck, Amir Yehudayoff |
| Journal | Submitted |
| Publication | July 2025 |
| Link | Read Article |
| Categories | Neural Networks, Complexity, Polytopes, Geometry |
We study approximations of polytopes in the standard model for computing polytopes using Minkowski sums and (convex hulls of) unions. Specifically, we study the ability to approximate a target polytope by polytopes of a given depth. Our main results imply that simplices can only be “trivially approximated”. On the way, we obtain a characterization of simplices as the only “outer additive” convex bodies. This translates to the inability to approximate functions with less depth in a certain model of computation using maximum-gate neural networks.
✧