Better Neural Network Expressivity: Subdividing the Simplex
| Authors | Egor Bakaev, Florestan Brunck, Christoph Hertrich, Jack Stade, Amir Yehudayoff |
| Journal | Submitted |
| Publication | May 2025 |
| Link | Read Article |
| Categories | Neural Networks, Complexity, Polytopes, Geometry |
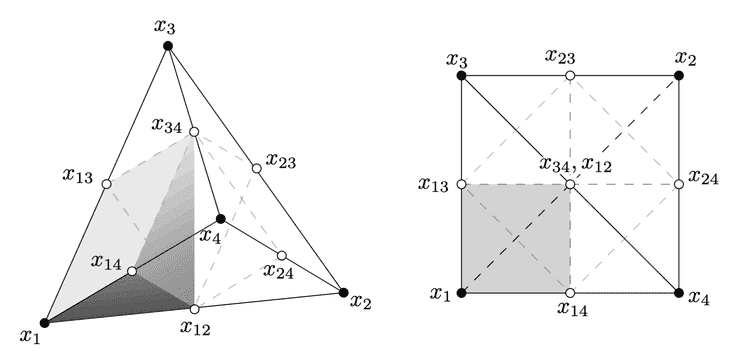
This work studies the expressivity of ReLU neural networks with a focus on their depth. A sequence of previous works showed that \mbox{} hidden layers are sufficient to compute all continuous piecewise linear CPWL functions on~. Hertrich, Basu, Di Summa, and Skutella (NeurIPS,‘21) conjectured that this result is optimal in the sense that there are CPWL functions on , like the maximum function, that require this depth. We disprove the conjecture and show that hidden layers are sufficient to compute all CPWL functions on .
A key step in the proof is that ReLU neural networks with two hidden layers can exactly represent the maximum function of five inputs. More generally, we show that hidden layers are sufficient to compute the maximum of numbers. Our constructions almost match the lower bound of Averkov, Hojny, and Merkert (ICLR,‘25) in the special case of ReLU networks with weights that are decimal fractions. The constructions have a geometric interpretation via polyhedral subdivisions of the simplex into “easier” polytopes.